Belajar Matematika dengan Tugas Bentuk Superitem

Biggs dan Collis (dalam Sumarmo 1993, h. 2) melakukan  studi tentang struktur hasil belajar dengan tes yang disusun dalam bentuk superitem. Biggs dan Collis dalam temuannya mengemukakan bahwa pada tiap tahap atau level kognitif  terdapat struktur respon yang sama dan makin meningkat dari yang sederhana sampai yang abstrak. Struktur tersebut dinamakan Taksonomi SOLO (Structure of the Observed Learning Outcome). Menurut Biggs dan Collis berdasarkan kualitas model respon anak, tahap SOLO anak diklasifikasikan pada empat tahap atau level.  Keempat tahap tersebut adalah unistruktural, multistruktural, relasional, dan abstrak.

Studi  tentang  tahap  SOLO,  juga  dilakukan  Sumarmo (1993).  Temuan dalam studi ini menguatkan keyakinan bahwa dalam pembelajaran   matematika, penjelasan konsep kepada siswa hendaknya tidak langsung pada konsep atau proses yang kompleks, tetapi harus dimulai dari konsep dan proses yang sederhana. Berdasarkan keyakinan tersebut, Sumarmo (1993) memberikan alternatif pembelajaran yang dimulai dari yang sederhana meningkat pada yang lebih kompleks. Pembelajaran tersebut menggunakan soal-soal bentuk superitem sebagai tugas.

Pembelajaran menggunakan tugas bentuk superitem adalah pembelajaran yang dimulai dari tugas yang sederhana meningkat pada yang lebih kompleks dengan memperhatikan tahap SOLO siswa. Dalam pembelajaran tersebut digunakan soal-soal bentuk superitem. Alternatif pembelajaran yang direkomendasikan Sumarmo tersebut, dirancang agar dapat membantu siswa dalam memahami hubungan antar konsep. Juga membantu dalam memacu kematangan penalaran siswa. Hal itu dilakukan agar siswa dapat memecahkan masalah matematika.

Sebuah  superitem  terdiri  dari  sebuah  stem yang  diikuti beberapa pertanyaan atau item yang semakin meningkat kekompleksannya. Biasanya setiap superitem terdiri dari empat item pada masing-masing stem. Setiap item menggambarkan dari empat level penalaran berdasarkan Taksonomi SOLO. Semua item dapat dijawab dengan merujuk secara langsung pada informasi dalam stem dan tidak dikerjakan dengan mengandalkan respon yang benar dari item sebelumnya. Pada level 1 diperlukan penggunaan satu bagian informasi  dari  stem. Level 2  diperlukan dua atau lebih bagian informasi dari stem.  Pada level 3 siswa harus mengintegrasikan dua atau lebih bagian dari informasi yang tidak secara  langsung  berhubungan  dengan  stem, dan pada level 4 siswa telah dapat mendefinisikan hipotesis yang diturunkan dari stem.

Karakteristik soal-soal bentuk  superitem yang memuat konsep dan proses yang makin tinggi tingkat kognitifnya tersebut, memberi peluang kepada siswa dalam mengembangkan pengetahuannya dan memahami hubungan antar konsep. Hal itu dikuatkan Lajoie (1991) yang menyatakan bahwa superitem didisain untuk mendatangkan penalaran matematis  tentang  konsep  matematika. Di samping itu soal bentuk superitem diharapkan lebih menantang dan mendorong keterlibatan siswa dalam pembelajaran. Sebaliknya guru dapat melakukan kegiatan diagnostik selama pembelajaran, sehingga perkembangan penalaran siswa dapat dimonitor lebih dini.

Kemampuan memahami hubungan antar konsep, kematangan dalam bernalar dan keterlibatan secara aktif dalam pembelajaran merupakan bagian yang diperlukan dalam memecahkan masalah. Dengan demikian pembelajaran menggunakan tugas bentuk superitem dapat diharapkan menjadi salah satu alternatif pembelajaran yang dapat membantu siswa dalam meningkatkan kemampuan meyelesaikan pemecahan masalah matematika.

Berikut ini tiga contoh butir tes bentuk superitem dengan tingkat kesulitan yang berbeda.  Soal disusun sedemikian rupa sehingga setiap butir tes memuat serangkaian informasi dan kemudian diikuti oleh empat pertanyaan  yang  sesuai  dengan  taksonomi  SOLO.

Contoh pertama dari Collis, Romberg dan Jurdak (dalam Sumarmo 1993) berikut,

 

Mesin di samping ini akan mengubah tiap bilangan yang masuk menjadi tiga kali lipat ditambah 2. Jadi bila dimasukkan bilangan 4 akan keluar bilangan 14.

Pertanyaan :

a. Jika keluar bilangan 14, bilangan berapa yang masuk?

b. Jika dimasukkan bilangan 5, bilangan berapa yang akan keluar?

c. Jika keluar bilangan 41, bilangan berapa yang masuk?

d. Jika x adalah bilangan yang keluar dan y adalah bilangan yang masuk,  nyatakan y dalam x.

Superitem yang kedua dikemukakan oleh Sumarmo (2002),

Perhatikan gambar berikut:

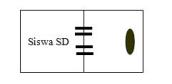
Sebuah ruangan mempunyai satu sekat dengan dua buah pintu. Seorang siswa harus pergi menuju sasaran dengan melalui pintu.

Pertanyaan:

1. Berapa banyak cara ia sampai ke sasaran? Bagaimana caranya?
2. Jika ada sekat kedua dengan dua pintu, berapa banyak cara ia sampai ke sasaran? Bagaimana caranya?
3. Jika ada empat sekat masing-masing dengan dua pintu, berapa banyak cara ia sampai ke sasaran? Bagaimana  caranya?
4. ika ada n sekat masing-masing dengan dua pintu, berapa banyak cara ia sampai ke sasaran? Bagaimana caranya?

Soal superitem ketiga, dicontohkan oleh Wilson dan  Chavarria ( 1993),

STEM

 

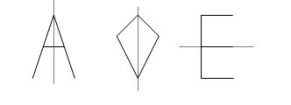
Jika gambar dapat dilipat sehingga menjadi dua bagian yang sama dan  tepat dipisahkan suatu garis lipatan, garis lipatan tersebut adalah garis simetri.

Gambar di atas mempunyai garis simetri yang lebih dari satu.

Pertanyaan :

a. Manakah gambar di bawah ini yang mempunyai garis simetri?

b. Gambarlah semua garis simetri pada persegi di bawah ini?

c. Manakah dari delapan huruf kapital pertama dalam alphabet mempunyai tepat dua garis simetri?

d. John berkata, “Saya tahu sebuah aturan untuk dapat memberitahukan, ketika sebuah gambar yang terdiri dari empat sisi mempunyai garis simetri. Jika sebuah segitiga pada masing-masing sisinya sama ukuran dan bentuknya, maka segitiga itu mempunyai garis simetri”. Jelaskan mengapa anda setuju atau tidak setuju dengan pendapat John!

Pada contoh soal ke-3 di atas, item a menggunakan hanya satu bagian dari informasi yang didapat secara langsung dari stem (definisi garis simetri). Pada item b, yang merupakan representasi dari level 2, siswa memerlukan penggunaan definisi dari garis simetri dan fakta gambar yang mempunyai lebih dari satu garis simetri. Sementara itu pada item c, menggunakan bagian informasi yang sama dari item b, tetapi  memerlukan kemampuan siswa dalam mengintegrasikan informasi yang menghasilkan diagram dan menggunakan definisi pada berbagai variasi dari kurva. Siswa dapat menyelesaikan soal item d, jika siswa dapat berfikir kritis tentang sebuah hipotesis yang diturunkan dari stem. Pada Taksonomi SOLO, item d ini termasuk ke dalam level4.

Berdasarkan contoh superitem di atas, dikandung maksud agar siswa memahami hubungan antar konsep secara bertahap dari yang sederhana sampai meningkat kepada yang lebih kompleks. Selain daripada itu guru melakukan kegiatan diagnostik terhadap respon siswa, sehingga dapat dengan segera menentukan langkah-langkah yang diperlukan dalam mencapai tujuan pembelajaran.

Kelebihan pembelajaran matematika dengan menggunakan tugas bentuk superitem diantaranya, dapat memberikan kesempatan kepada siswa untuk memahami persoalan matematika secara bertahap sesuai kesiapannya; dan guru dapat memberikan bantuan yang tepat kepada siswa berdasarkan respon dari siswa. Pada sisi lain pembelajaran ini akan memberi kesulitan kepada guru dalam membuat atau menyusun butir-butir soal  bentuk superitem. Kemudian dimungkinkan terdapat respon siswa yang

beragam.  Hal itu akan menuntut kesiapan guru dalam mengantisipasinya.

Wilson dan Chavarria (1993) memberikan pengalamannya dalam mengkonstruksi bentuk soal superitem yaitu,

1. Mengkonstruksi sebuah superitem akan dimulai dengan menentukan terlebih dahulu prinsip umum apa yang akan menjadi fokus pada item level empat. Prinsip tersebut akan dibangun oleh tiga item sebelumnya. Setiap item akan membantu siswa dalam menggali situasi dari masalah.
2. Stem akan menyajikan sebuah masalah yang relevan dan diperlukan siswa.
3. Respon dari setiap item di dalam sebuah superitem tidak bergantung pada respon yang benar dari item sebelumnya.

Pengalaman kedua ahli tersebut, tampaknya dapat membantu guru dalam menyusun butir soal bentuk superitem.

Untuk mengetahui pengertian, langkah-langkah , kelebihan dan kekurangan model pembelajaran superitem klik  Model Pembelajaran Superitem

 

DAFTAR PUSTAKA:

Lajoie,S (1991). A Framework for Authentic Assessment in Mathematics. [Online].Tersedia: http://www.wcer.wisc.edu/ncisla/publications/newsletters/normse/vol1num.1pdf.
http://madfirdaus.wordpress.com/2009/11/17/tugas-matematika-bentuk-superitem/

Sumarmo,U (1993). Profil Struktur Hasil Belajar Matematika Siswa SMA Berdasarkan Taksonomi SOLO. Laporan Hasil Penelitian FPMIPA IKIP Bandung

Sumarmo,U (2002). Alternatif Pembelajaran Matematika dalam Menerapkan Kurikulum Berbasis Kompetensi . Makalah pada Seminar Matematika Tingkat Nasional. Bandung

Wilson dan Chavarria (1993). Superitem Test as a Classroom Assessment Toll. Dalam Webb dan Coxford  (ed). Assessment in the Mathematics Classroom 1993 Yearbook. NCTM: Reston Virginia